The p-Chart, also known as the Percent (or Fraction) Defective Parts Chart, and Percent (or Fraction) Nonconforming Parts Chart, is the most common of the Attribute Control Charts. For a sample subgroup, the number of defective parts is counted and plotted as either a percentage of the total subgroup sample size, or a fraction of the total subgroup sample size. The p-Chart chart can be used if the sample subgroup size varies from sampling interval to sampling interval. In this case, the control chart high and low limits vary from sample interval to sample interval, depending on the number of samples in the associated sample subgroup. A low number of samples in the sample subgroup make the band between the high and low limits wider than if a higher number of samples are available. Both the Fraction Defective Parts and Percent Defective Parts control charts come in versions that support variable sample sized for a subgroup.
Note that this chart tracks the number of defective parts, not the number of defects as done in the c-chart. Therefore there must be some yes/no decision of whether or not the sampled part meets production standards. A defective part does not indicate any magnitude of defectiveness (such as might be measured in one of the variable control charts), only that it is, or is not defective.
p-Chart (percentage) – 1
p-Chart (fraction) – 1
Sample subgroup size = 50
Defect data = { 12, 15, 8, 10, 4, 7, 16, 9, 14, 10, 5, 6, 17, 12, 12, 8, 10, 5, 13, 11, 10, 18, 14, 15, 9, 12, 7, 13, 9, 6}
The data used in the chart is based on the non-conforming control chart example, Table 7-1, in the textbook Introduction to Statistical Quality Control 7th Edition, by Douglas Montgomery. Several of the values which exceeded the control limits were modified, to make this set of data an in-control run, suitable for calculating control limits.
The p-chart (percentage), p-chart (fraction), and np-chart are basically the same chart. The only difference is how the display data is normalized. The p-chart (percentage) normalizes the defect data as a % (0-100%) of the sample subgroup size for the current sample interval. The p-chart (fraction) normalizes the defect data as a fraction (0.0 – 1.0) of the sample subgroup size for the current sample interval. And the np-chart does away with the normalization and just plots the raw defect data. For example, if the sample size for a sample interval is 50 and the number of defects is 11, then the p-chart (percentage) value is 22%, the p-chart (fraction) value is 0.22 and the np-chart value is 11.
The limits are calculated accordingly. Because of the normalization by sample subgroup size that takes place on every sample interval, it is easier to support varying sample subgroup size in p-charts (fraction and percentage) and that gives them an advantage when compared to the np-chart.
If you know the standard value of the fraction non-conforming (p) you can use that in the control limit formulas. If not, you will need to calculate an approximate value using the data available in a sample run while the process is operating in-control. In that case the value of p will be referred to as \(\bar{p}\).
Let (\(D_1, D_2, …, D_N\)) be the defect counts of the N sample intervals, where the sample subgroup size is M. The total nonconforming count is the sum of the D-values. The \(\bar{p}\) (fraction nonconforming) is given by the equation.
\(\Large{p \approx \bar{p}=\left[{\frac{\sum_{j=1}^N D_j}{M * N}}\right]}\)Control Limits for the p-Chart
p-Chart (fraction defective parts)
\(\large{UCL= p + 3 * \sqrt{p * \frac{(1-p)}{M}}}\) \(\large{Center line = p}\) \(\large{LCL= p – 3 * \sqrt{p * \frac{(1-p)}{M}}}\)p-Chart (percent defective parts)
\(\large{UCL= 100\% * \left[{p + 3 * \sqrt{p * \frac{(1-p)}{M}}}\right]}\) \(\large{Center line = 100\% * p}\)
\(\large{LCL= 100\% * \left[{p – 3 * \sqrt{p * \frac{(1-p)}{M}}}\right]}\)
where :
\({p \approx \bar{p} =}\) estimate (or average) of the fraction defective (or non-conforming) partsM = number of samples per subgroup
Note that in the p-Chart formulas, the there is no explicitly calculated sigma value. That is because attribute charts in general assume a binomial distribution about the mean. In a binomial distribution, the sigma value of the distribution is characterized using only the mean of the distribution, using the formula below, where the value p is the value for the fraction of non-conforming parts. You find this expression in the formulas for the UCL and LCL control limits.
\(\Large{\sigma = \sqrt{\left[{\frac{p(1-p)}{N}}\right]}}\)p-Chart (percent defective parts) – 2 (Interactive)
The initial chart represents a sample run where the process is considered to be in control. Therefore it is a suitable source of data to calculate the UCL, LCL and Target control limits. The control limit lines and values displayed in the chart are a result these calculations. What you don’t want to do is constantly recalculate control limits based on current data. Because once the process goes out of control, you will be incorporating these new, out of control values, into the control limit calculations, which will widen the control limits. Instead, as you move forward, you apply the previously calculated control limits to the new sampled data. When the process starts to go out of control, it should produce alarms when compared to the control limits calculated when the process was in control. You can simulate this using the interactive chart above.
When you select the Simulate Data button in the p-Chart(Fraction Defective Parts) -2 chart above, the dialog below appears:
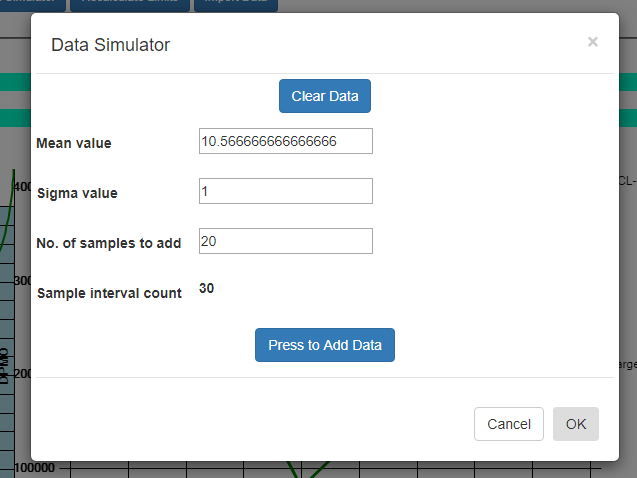
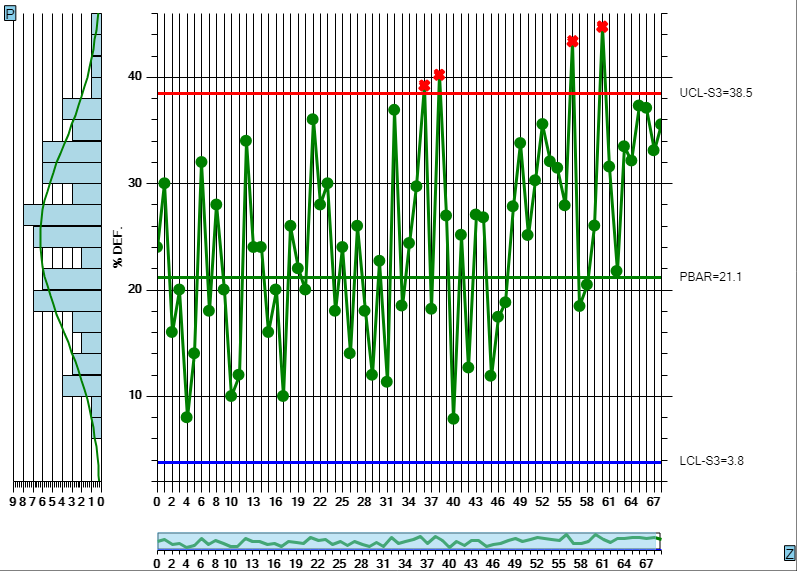
What it shows for the Mean value is the value calculated based on the current data. The sigma value does not apply since the simulated data for attribute charts are derived from the mean value. So if you simulate new sample intervals using these values, the result will be that the new values look like the old, and the process will continue to stay within limits. Even using these values, you will, however, get a random control limit violation on the order of every 1 in every 370 sample intervals. This is known as a false positive (alarm) and it is due to the probabilistic nature of SPC control charts. See the section on Average Run Length (ARL) for more details. But if you modify the Mean value slightly, you increase the odds, above that of the ARL value, that the process exceeds the pre-established control limits and generates an alarm. So change the Mean value to 14. Now you are simulating the process has changed enough to alter the both the mean and variability of the process variable under measurement. Press the Press to Add Data button a couple of time to generated the simulated values, then exit the dialog by pressing OK. The new data values are appended to the existing data values, and you should be able to see the change starting at the 30th sample interval. Use the scrollbar at the bottom of the chart to scroll to the start of the simulated data. The picture below displays the simulation. Your picture may not look exactly the same, because the simulated data values are randomized, and your randomized simulation data will not match the values in the picture. But the general idea will be the same. You find a more generalized, and detailed discussion of how to work with the Interactive charts here:
If you want to try and plot your own data in the p-Chart chart, you should be able to do so using the Import Data option of the Interactive chart. Organize your data in a spreadsheet, where the rows represent sample intervals and the columns represent samples within a subgroup. Make sure you only highlight the actual data values, not row or column headings, as in the example below.
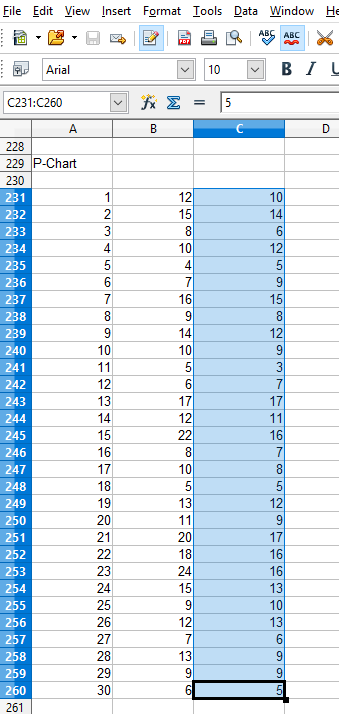
Copy the rectangle of data values from the spreadsheet and Paste them into the Data input box. By default, data values copied from a spreadsheet should be column delimited with the TAB character, and row delimited with the LF (LineFeed) character. If so, our Data input box should be able to parse the data for chart use.
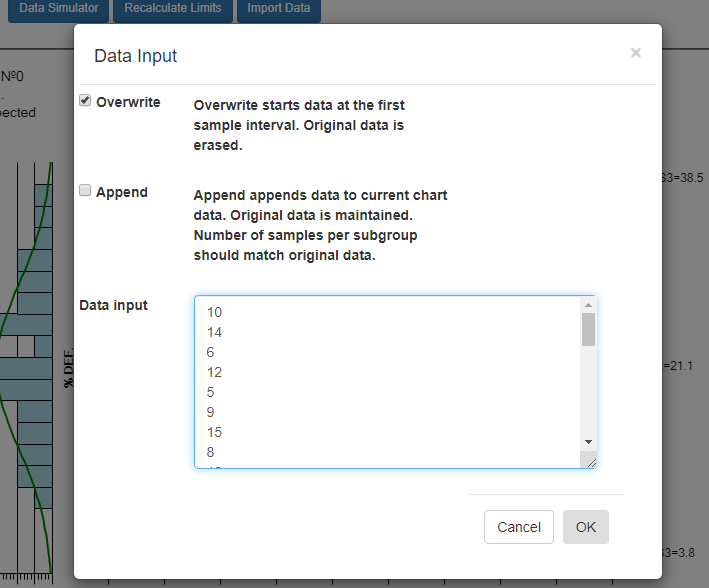
Select OK, and if the data parses properly you should see the resulting data in the chart. By default, data entered into the Data input box overwrites all of the existing data. That way you can create your own custom p-Chart chart, using only your own data. You start by entering in a batch of data
from an “in control” run of your process, and display the data in a new chart. Calculate new control limits based on this data, using the Recalculate Limits button. Should you want to enter in another batch of actual data from a recent run, and append it to the original data, go back to the Import Data menu option. This time select the Append checkbox instead of the default Overwrite data checkbox.
General Issues with p-Chart
Attribute charts generally assume that the underlying data approximates a binomial distribution. That is to say that the values of the data can be characterized as a function of fn(mean, N), where N represents the sample population size, and mean is the average of those sample values. Logically that forms the basis for looking for an out of control process by checking if the sample value for a sample interval are outside the 3-sigma limits of the process when it is under control.
If you are using a fixed sample subgroup size, you will need to make the subgroup size large enough to be statistically significant. You want the sample size to be large enough that you usually have at least one non-conforming part per sample interval, otherwise you will generate false alarms if you leave an LCL of 0.0 (which is possible) enabled. One possibility is to set the sample size large enough to produce a non-zero LCL (most of the time), using the formula: \({M>{\frac {3^{2}(1-{\bar {p}})}{\bar {p}}}}\), where M is the subgroup sample size. Another option is set the sample rate high enough to detect a specified shift in the process at least half the time. For the standard 3-sigma UCL and LCL control limits, the formula is \({\displaystyle M\geq \left({\frac {3}{\delta }}\right)^{2}{\bar {p}}(1-{\bar {p}})}\), where \(\delta\) is the shift in the process mean you want to detect. For example, if p = 0.01, and you want to detect a shift in the process from 0.01 to 0.05 ( \(\delta = 0.04\)) non-conforming, the equation would produce \({\displaystyle M\geq \left({\frac {3}{0.04 }} \right)^{2}* {0.01} * (1-{0.01}) = 56 }\)
p-Charts Charts with Variable Sample Size
If a variable subgroup sample size, from sample interval to sample interval, is a requirement, you can still use the p-Chart, both the fraction and percentage versions. The UCL and LCL values need to be recalculated for every sample interval. The fewer the samples for a given sample interval, the wider the resulting UCL and LCL control limits will be. In order for the chart to be worthwhile, you should still maintain a minimum sample size in accordance with your predetermined goals.
p-Chart with variable subgroup sample size (Fraction Defective Parts)
\(\large{UCL= p + 3 * \sqrt{p * \frac{(1-p)}{M_i}}}\) \(\large{Center line = p}\) \(\large{LCL= p – 3 * \sqrt{p * \frac{(1-p)}{M_i}}}\)where the sample subgroup size at interval i is\( M_i\).
The formulas for the p-Chart (percentage) are the same, except you multiple the resultant LCL and UCL values by 100%.
Run a version of the p-Chart chart which supports variable sample size.
p-Chart (fraction) – Variable Sample Subgroup Size (Interactive)
Note that the control limits vary with the subgroup sample size, widening for sample intervals which have a lower subgroup sample size.
You can enter your own data which has a varying subgroup size using the Data Import option. Copy it from a spreadsheet where the unused columns are just left empty.
You can enter data which has a varying subgroup size using the Data Import option. In this case you need a two column format. The first column holds the defective parts number for the sample interval, and the second column holds the sample subgroup size for that sample interval.

Paste it into the Data Import Input table. When the OK button is selected, it should parse into a p-Chart chart with variable subgroup sample size (VSS for short).