You will find the XBar-Sigma chart listed under may different names, including: XBar-S, Mean-Sigma, XBar and Sigma, \(\bar{X}\) and Sigma, Average-Sigma, and Mean-Sigma. A typical XBar-Sigma chart consists of two graphs displayed one above the other. The top graph is the XBar chart, and the bottom graph is the Sigma chart. The example below shows a typical XBar-Sigma chart.
XBar-Sigma Chart – 1
The data used in the chart is based on the XBar-Sigma chart example, Table 6-3, in the textbook Introduction to Statistical Quality Control 7th Edition, by Douglas Montgomery. Since this is a XBar-Sigma chart, the number of samples per subgroup was increased to 9, to better reflect a dataset that chart type is used with.
The XBar-Sigma chart is one of several chart types which fall under the general category known as Shewhart Control Charts, which is a general grouping of SPC chart types that work with quality data expressed as numeric values (i.e. 72.623412). The XBar-Sigma chart monitors the trend of a critical process variable over time using a statistical sampling method that results in a subgroup of values at each subgroup interval. The XBar part of the chart plots the mean of each sample subgroup and the Sigma part of the chart monitors the standard deviation of the values within each sample interval. Superimposed control lines indicate whether or not the process being monitored is in or out of statistical control.
Statistically an XBar-Sigma chart makes the most sense if you monitoring a process variable which can be sampled using a fixed subgroup size. The fixed subgroup size should be 9 or greater samples. For example, every 15 minutes you pull 12 items (out of 1000 produced in the same time period) off the line, measure them, and record the values as the samples for the subgroup at that sample interval. In that case the sample subgroup size would be 12. The XBar-Sigma chart will still calculate for subgroup sizes greater less than 9, but typically the XBar-R chart is used in those cases. The XBar-Sigma chart will not work if you use a subgroup size of 1, because that will always result in an undefined Sigma. The denominator value in the Standard Deviation calculation is (subgroup size – 1) and that won’t work if the subgroup size is 1 . The Individual-Range chart (I-R chart for short) works around this limitation and you need to use it if you have a sample subgroup size of 1. Also, if you are running crude tests of your SPC chart, and use a sample subgroup size of greater than 8, but for each sub interval enter the same value, that too will fail. Anything which results in a 0.0 Sigma value across all sample intervals is going to render the control limit calculations invalid. You can have a sample interval with a 0.0 range and that will most likely generate control limit violation for that sample interval in the Sigma-chart. But all sample intervals can’t have 0.0 variation.
The initial setup of the chart typically involves establishing standardized control UCL (Upper Control Limit) and LCL (Lower Control Limit), and Target (Centerline) values, for both the Primary (XBar) and Secondary (Seconday) charts. These limits are calculated based on monitoring and sampling the process when it is running while “in control”. The formulas for XBar-Sigma charts are listed below.
Each sample interval has M values, representing the sample subgroup size. The mean \({\bar{X_i}}\) or (XBar i value) for each sample interval is just the standard mean calculation using the data values
(\(X_1, X_2, …, X_M\)) for that sample interval.
Let (\(\bar{X_1}, \bar{ X_2}, …, \bar{ X_M}\)) be the means of the N sample intervals. The \(\bar{\bar{X}}\) (mean of means, or XBarBar) is just the mean of the N \(\bar{X}\) ( or XBar), values.
\(\Large{\bar{\bar{X}}=\left(\frac{1}{N}\right)\sum_{i=1}^N \bar{X_i} = \frac{(\bar{X_1} + \bar{X_2} + \cdots + \bar{X_N})}{N}}\)The calculations for the XBar part of this chart is the same as for the XBar-R chart, since they both plot the mean of the sample subgroups.
Let (\(S_1, S_2, … S_N\)) be the sigma values (standard deviation) of the N sample intervals. The sigma for each sample interval (of subgroup size M) is calculated using the sample standard deviation formula.
\(\Large{S = \sqrt{\frac{1}{M-1} \sum_{i=1}^M (X_i – \overline{X})^2}} \)The \(\bar{S}\) (or SBar) value is calculated as the mean of the individual sigma values for each of the N sample intervals.
\(\Large{\bar{S}=\left(\frac{1}{N}\right)\sum_{i=1}^N S_i = \frac{(S_1 + S_2 + \cdots + S_N)}{N}}\)Assume that the test data in the chart above is such a run. You will find the raw sample data (5 samples per subinterval (M), 25 subintervals (N)) in the table section of the chart below in the Sample No1 to Sample No5 rows. The Mean row shows the calculated Mean ( \({\bar{X_i}}\)) values for each sample interval. The Sigma row shows the calculated Sigma ( \(S_i\)) value for each sample interval. These values are used to calculate the \({\bar{\bar{X_i}}}\) and \({\bar{S}}\) values use in the charts Target, LCL and UCL formulas.
Control Limits for the Xbar – top chart
\(\Large{UCL= \bar{\bar{X}} + A_3 * \bar{S} }\\\) \(\Large{Target = \bar{\bar{X}}}\\\) \(\Large{LCL= \bar{\bar{X}} – A_3 * \bar{S}}\\\)where the constant A3 is tabulated in Table XBar-Sigma Chart Factors table below.
Control Limits for the Sigma (S) – bottom chart
\(\Large{UCL= B_4 * \bar{S} }\) \(\Large{Target = \bar{S} }\) \(\Large{LCL= B_3 * \bar{S} }\)where the constants B3 and B4 are tabulated for various sample sizes in the Table of XBar-Sigma Chart Factors table below.
Table of XBar-Sigma Chart Factors
| Subgroup Size | A3 | B3 | B4 |
| 2 | 2.659 | 0 | 3.267 |
| 3 | 1.954 | 0 | 2.568 |
| 4 | 1.628 | 0 | 2.266 |
| 5 | 1.427 | 0 | 2.089 |
| 6 | 1.287 | 0.03 | 1.97 |
| 7 | 1.182 | 0.118 | 1.882 |
| 8 | 1.099 | 0.185 | 1.815 |
| 9 | 1.032 | 0.239 | 1.761 |
| 10 | 0.975 | 0.284 | 1.716 |
| 11 | 0.927 | 0.321 | 1.679 |
| 12 | 0.886 | 0.354 | 1.646 |
| 13 | 0.85 | 0.382 | 1.618 |
| 14 | 0.817 | 0.406 | 1.594 |
| 15 | 0.789 | 0.428 | 1.572 |
| 16 | 0.763 | 0.448 | 1.552 |
| 17 | 0.739 | 0.466 | 1.534 |
| 18 | 0.718 | 0.482 | 1.518 |
| 19 | 0.698 | 0.497 | 1.503 |
| 20 | 0.68 | 0.51 | 1.49 |
| 21 | 0.663 | 0.523 | 1.477 |
| 22 | 0.647 | 0.534 | 1.466 |
| 23 | 0.633 | 0.545 | 1.455 |
| 24 | 0.619 | 0.555 | 1.445 |
| 25 | 0.606 | 0.565 | 1.435 |
XBar-Sigma Chart – 2 (Interactive)
The control limits in this example are slightly different that those calculated in the textbook Introduction to Statistical Quality Control 7th Edition, by Douglas Montgomery, because our dataset uses a large sample subgroup size (9), filled with randomized data.
The initial chart represents a sample run where the process is considered to be in control. Therefore it is a suitable source of data to calculate the UCL, LCL and Target control limits. The control limit lines and values displayed in the chart are a result these calculations. What you don’t want to do is constantly recalculate control limits based on current data. Because once the process goes out of control, you will be incorporating these new, out of control values, into the control limit calculations, which will widen the control limits. Instead, as you move forward, you apply the previously calculated control limits to the new sampled data. When the process starts to go out of control, it should produce alarms when compared to the control limits calculated when the process was in control. You can simulate this using the interactive chart above.
When you select the Simulate Data button in the XBar-Sigma Chart-2 chart above, the dialog below appears:
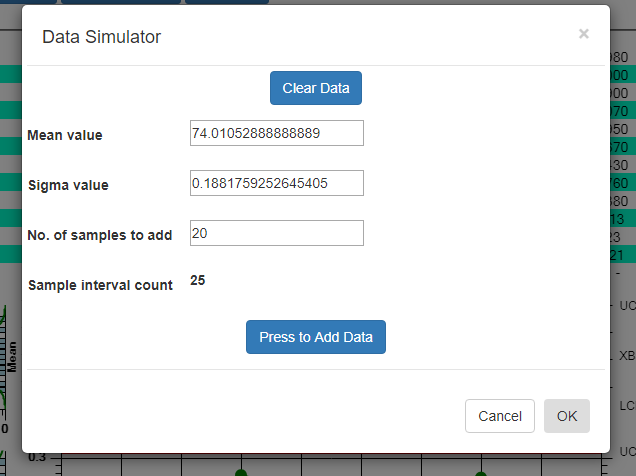
What it shows for the Mean value and Sigma value are the values calculated based on the current data. So if you simulate new sample intervals using these values, the result will be that the new values look like the old, and the process will continue to stay within limits. Even using these values, you will, however, get a random control limit violation on the order of every 1 in every 370 sample intervals. This is known as a false positive (alarm) and it is due to the probabilistic nature of SPC control charts. See the section on Average Run Length (ARL) for more details. But if you modify the Mean and/or the Sigma value slightly, you increase the odds, above that of the ARL value, that process exceeds the pre-established control limits and generates an alarm. So change the Mean value to 74.21, and the Sigma Value to 0.228. Now you are simulating the process has changed enough to alter the both the mean and variability of the process variable under measurement. Press the Press to Add Data button a couple of time to generated the simulated values, then exit the dialog by pressing OK. The new data values are appended to the existing data values, and you should be able to see the change starting at the 26th sample interval. Use the scrollbar at the bottom of the chart to scroll to the start of the simulated data. The picture below displays the simulation. Your picture may not look exactly the same, because the simulated data values are randomized, and your randomized simulation data will not match the values in the picture. But the general idea will be the same. You find a more generalized, and detailed discussion of how to work with the Interactive charts here:

If you want to try and plot your own data in the XBar-Sigma chart, you should be able to do so using the Import Data option of the Interactive chart. Organize your data in a spreadsheet, where the rows represent sample intervals and the columns represent samples within a subgroup. Make sure you only highlight the actual data values, not row or column headings, as in the example below.
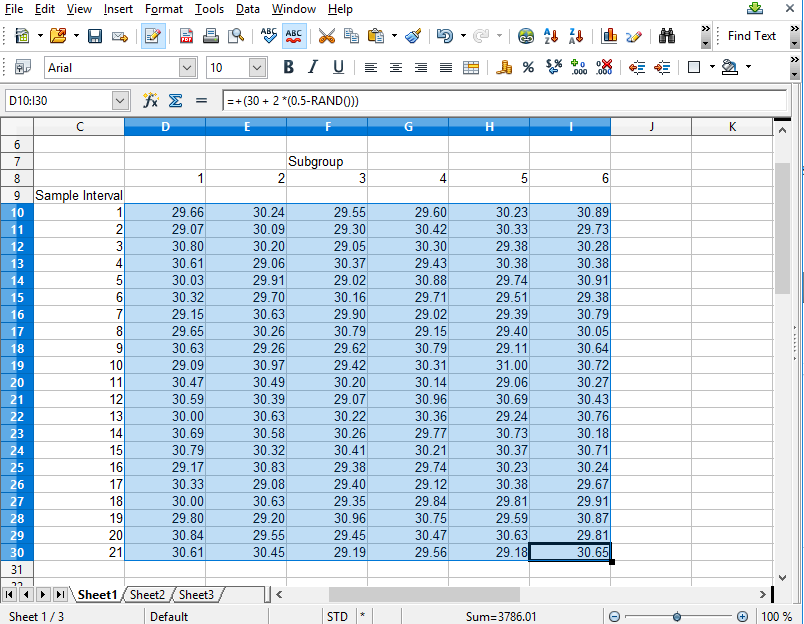
Copy the rectangle of data values from the spreadsheet and Paste them into the Data input box. By default, data values copied from a spreadsheet should be column delimited with the TAB character, and row delimited with the LF (LineFeed) character. If so, our Data input box should be able to parse the data for chart use.
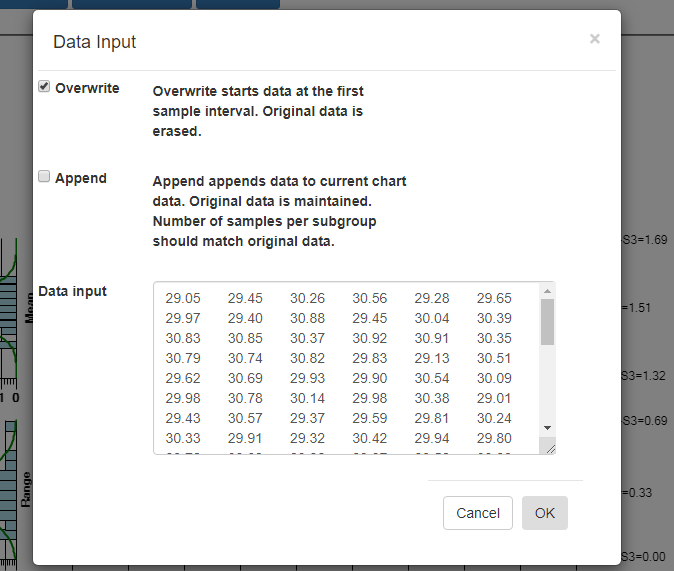
Select OK, and if the data parses properly you should see the resulting data in the chart. By default, data entered into the Data input box overwrites all of the existing data. That way you can create your own custom XBar-R chart, using only your own data. You start by entering in a batch of data
from an “in control” run of your process, and display the data in a new chart. Calculate new control limits based on this data, using the Recalculate Limits button. Should you want to enter in another batch of actual data from a recent run, and append it to the original data, go back to the Import Data menu option. This time select the Append checkbox instead of the default Overwrite data checkbox.
General Issues with XBar-Sigma Chart
XBar-Sigma charts generally assume that the underlying data approximates a normal distribution. That is to say that the values of the data can be characterized using a mean and sigma (standard deviation) value. Logically that forms the basis for looking for an out of control process by checking if average sample values for a sample subinterval are outside the 3-sigma limits of the process when it is under control. But real world sample data may not me strictly normal. There are a many different statistical distributions (normal, Poisson, binomial, hyper-geometric) which can be used to model the variation in sample data. In general, unless your data is extremely skewed, all of the averaging within sample intervals, and across sample intervals, will produce approximately normal results because of the Central Limit Theorem, which loosely states that sample subgroup means will produce a normal distribution about the overall population mean, even if the values within each sample subgroup are not normal.
Sigma Charts with Variable Sample Size
If a variable subgroup sample size, from sample interval to sample interval, is a requirement, then you need to either use an XBar-Sigma chart with variable sample size, or an Individual-Range chart, which always assumes the sample subgroups size is one. In the case of the Individual-Range chart, each sample would take up one sample interval, so the subgroups sample size would be one. If you are using an XBar-Sigma chart with variable sample subgroup size, the Target, UCL and LCL formulas change, and the UCL and LCL value need to be recalculated for every sample interval. The fewer the samples for a given sample interval, the wider the resulting UCL and LCL control limits will be.
Formula for the \({\bar{\bar{X}}}\) value in a XBar-Sigma chart with variable sample size, where \({M_i}\) is the sample size for each sub interval, and there are n sample intervals.
\(\Large{{\bar{\bar {X}}}={\frac {\sum \limits _{i=1}^{N}M_i \bar{X}_i}{\sum \limits _{i=1}^{N}M_i}}}\)Formula for the \({\bar{S}}\) value in a XBar-Sigma chart with variable sample size, where \({M_i}\) is the sample size for each sub interval, and there are N sample intervals.
\(\Large{{\bar {S}}=\sqrt{\left({\frac {\sum \limits _{i=1}^{N}(M_i – 1)S_i ^2}{{(\sum \limits _{i=1}^{N}M_i })-N}}\right)}}\)XBar-Sigma Variable Control Limits for the Xbar (top) chart
\(\Large{UCL= \bar{\bar{X}} + A_3 * \bar{S} }\\\) \(\Large{Target = \bar{\bar{X}}}\\\) \(\Large{LCL= \bar{\bar{X}} – A_3 * \bar{S}}\\\)where \({\bar{\bar{X}}}\) and \({\bar{S}}\) are calculated using the weighted average techniques above, and the constant A3 varies depending on the sample subgroup size for the current sample interval, as tabulated in the Table XBar-Sigma Chart Factors table in the previous section.
XBar-Sigma Variable Control Limits for the Sigma (bottom) chart
\(\Large{UCL= B_4 * \bar{S} }\) \(\Large{Target = \bar{S} }\) \(\Large{LCL= B_3 * \bar{S} }\)Run a version of the XBar-Sigma chart which supports variable sample size.
XBar-Sigma Chart – Variable Sample Subgroup Size (Interactive)
Note that the control limits vary with the subgroup sample size, widening for sample intervals which have a lower subgroup sample size.
You can enter your own data which has a varying subgroup size using the Data Import option. Copy it from a spreadsheet where the unused columns are just left empty.
You can enter data which has a varying subgroup size using the Data Import option. Copy it from a spreadsheet where the unused columns are just left empty.
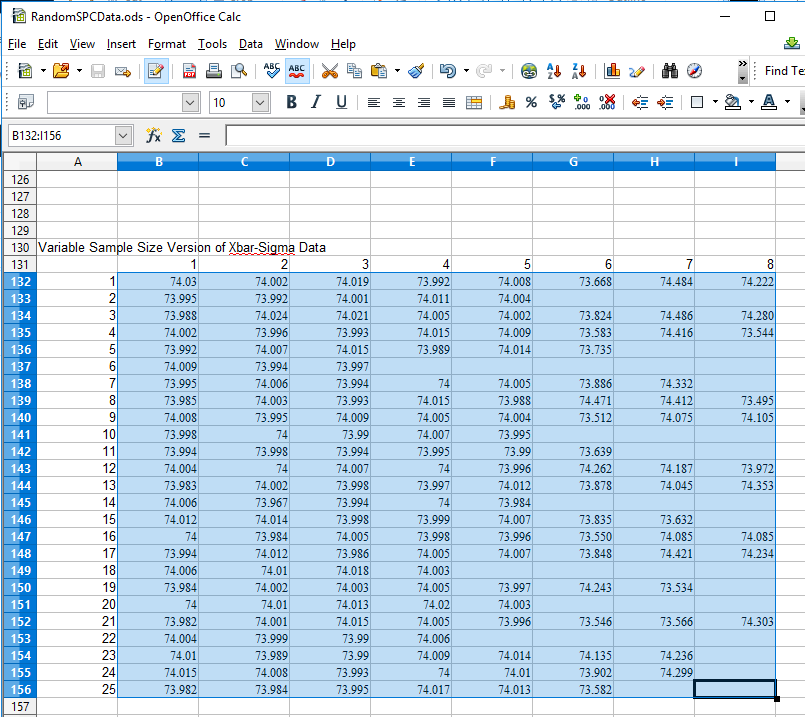
Paste it into the Data Import Input table. When the OK button is selected, it should parse into a XBar-Sigma chart with variable subgroup sample size (VSS for short).
where \({\bar{\bar{X}}}\) and \({\bar{S}}\) are calculated using the weighted average techniques above, and the constants B3 and B4 vary depending on the sample subgroup size for the current sample interval, as tabulated in the Table XBar-Sigma Chart Factors in the previous section.